Statistics [03]: Some Common Discrete Distributions

4 minute read

Published: January 03, 2021

This post will summarize some of the commonly used discrete distributions, including

Uniform distribution
Bernoulli distribution
Binomial distribution
Geometric distribution
Negative binomial distribution
Poisson distribution
Hypergeometric distribution
Mulitnomial distribution.

Uniform Distribution

The discrete uniform distribution is also known as the “equally likely outcomes” distribution. Letting a set $S$ have $N$ elements, each of them having the same probability. Then, the probability distribution function and cumulative distributions function are respectively

$P(n) = \dfrac{1}{N}$

$D(n) = \dfrac{1}{N}$

Bernoulli Distribution

The Bernoulli distribution is a discrete distribution having two possible outcomes labelled by $n=0$ and $n=1$ in which $n=1$ occurs with probability $p$ and $n=0$ occurs with probability $q = 1 - p$ . Therefore, it has probability density function

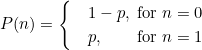
drawing

which can also be written as

$P(n) = p^n(1-p)^{1-n}$

The cumulative distribution function is

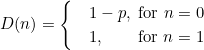
The performance of a fixed number of trials with fixed probability of success on each trial is known as a Bernoulli trial.

The distribution of heads and tails in coin tossing is an example of a Bernoulli distribution with $p=q=1/2$ . The probability of A winning each game in the example give in this post is an example of Bernoulli distribution with $p=p, q=1-p$ .

The Bernoulli distribution is the simplest discrete distribution, and it the building block for other more complicated discrete distributions.

Binomial Distribution

The binomial distribution gives the discrete probability distribution $P_p(n\,|\,N)$ of obtaining exactly $n$ successes out of $N$ Bernoulli trials. The binomial distribution is therefore given by

$P_p(n\,|\,N) = \dbinom{N}{n} p^nq^{N-n} = \dfrac{N!}{n!(N-n)!}p^nq^{N-n}$

Given the binomial distribution, the probability of obtaining more successes than the $n$ observed in a binomial distribution is

$P(X>n) ={\displaystyle\sum_{k=n+1}^N\dbinom{N}{k}p^k(1-p)^{N-k} = I_p(n+1, N-n)}$

where

$I_p(a, b) = \dfrac{B(p;a,b)}{B(a,b)}$

$B(a,b)$ is the beta function, and $B(p;a,b)$ is the incomplete beta function, with

$B(a,b) = \dfrac{(a + b - 1)!}{(a-1)!(b-1)!}$

and

$B(p;a,b) = {\displaystyle \int_0^px^{a-1}(1-x)^{b-1}dx}$

To prove the above relationship, first differentiate both sides wrt $p$ .

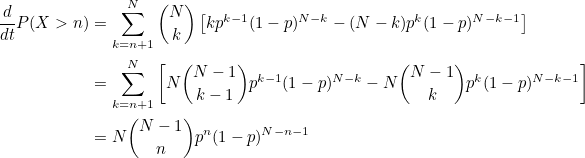
Then integrate, we get

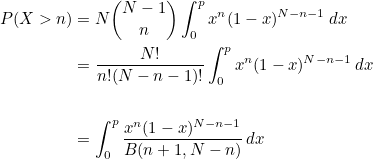
Geometric Distribution

The geometric distribution gives the discrete probability distribution $P(n)$ of obtaining exactly $n$ failures of Bernoulli trials before first success. The geometric distribution is therefore given by

$P(n) = p(1-p)^n = pq^n$

The cumulative distribution function is

$D(n) = {\displaystyle\sum_{k=0}^nP(k) = p\dfrac{1 - q^{n+1}}{1 - q} = 1 - q^{n+1}}$

The geometric distribution is memoryless. It is a discrete analog of the exponential distribution.

Negative Binomial Distribution

The negative binomial distribution is a combination of binomial distribution and geometric distribution, which gives the probability of $r-1$ successes and $x$ failures in $x+r-1$ trials, and success on the $(x+r)\text{th}$ trial. The probability density function is therefore given by

$P_{p\text{,}r}(x) = p\left[\dbinom{x+r-1}{r-1}p^{r-1}(1-p)^{x}\right] = \dbinom{x+r-1}{r-1}p^r(1-p)^{x}$

The cumulative distribution function is (Proof?)

$D(x) = {\displaystyle \sum_{n=0}^x\dbinom{n+r-1}{r-1}p^r(1-p)^{n} = I_p(r, x+1)}$

The negative binomial distribution gets its name from the following relationship (Proof):

$\dbinom{k+r-1}{k} = (-1)^k\dbinom{-r}{k}$

With this relationship, we have

$\sum_{n=0}^\infty\dbinom{n+r-1}{r-1}p^r(1-p)^{n} = p^r\sum_{n=0}^\infty\dbinom{n+r-1}{n}(1-p)^{n} = p^r\sum_{n=0}^\infty\dbinom{-r}{n}(-1)^n(1-p)^{n} = p^rp^{-r} = 1$

Poisson Distribution

Possion distribution is often used to describe comparatively rare cases, and when the $N$ becomes very large in binomial distribution, possion distribution can be a good approximation.

Viewing the binomial distribution as a function of the expected number of successes

$\nu = Np$

instead of the sample size $N$ for fixed $p$ . Then, the equation for binomial distribution becomes

$P_{\nu\text{/}N}(n\,|\,N) \dfrac{N!}{n!(N-n)!}\left(\dfrac{\nu}{N}\right)^n\left(1 - \dfrac{\nu}{N}\right)^{N-n}$

Letting the sample size N become large, the distribution then approaches

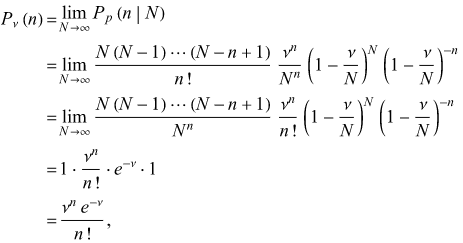
which is known as the Poisson distribution.

Hypergeometric Distribution

Let there be $n$ ways for a “good” selection and $m$ ways for a “bad” selection out of a total of $n + m$ possibilities. Take $N$ samples and let $x_i$ equal 1 if selection $i$ is successful and 0 if it is not. Let $x$ be the total number of successful selections,

$x = {\displaystyle \sum_{i=1}^Nx_i}$

The probability of $i$ successful selections is

$P(x=i) = \dfrac{\dbinom{n}{i}\dbinom{m}{N-i}}{\dbinom{m+n}{N}}$

Multinomial Distribution

Let a set of random variates $X_1, X_2, ..., X_n$ have a probability function

$P(X_1=x_1, ..., X_n=x_n) = \dfrac{N!}{\prod_{i=1}^{n}x_i}\prod_{i=1}^n\theta_i^{x_i}$

and $\theta_i$ are constants with $\theta_i>0$ and

$\sum_{i=1}^n\theta_i = 1$

Then the joint distribution of $X_1, X_2, ..., X_n$ is a multinomial distribution and $P(X_1=x_1, ..., X_n=x_n)$ is given by the corresponding coefficient of the multinomial series

$(\theta_1 + \theta_2 + ... + \theta_n)^N$

Twitter Facebook LinkedIn

Chao Huang