Statistics [06]: Order Statistics

1 minute read

Published: January 06, 2021

Two simple examples of order statistics.

Example 1

Suppose $X_1, X_2, ..., X_n$ are independent homogeneous distribution, which have density function $p(x)$ and distribution function $F(x)$ . Now order the $n$ variables in the following way

$X_{(1)}\leq X_{(2)}\leq ... \leq X_{(n)}$

What would the distribution of $X_{(k)}$ be like?

Assume the probability of $X_{(k)}$ lying in $[x, x+\Delta x]$ is

$F_k(x+\Delta x) - F_k(x) = \dfrac{n!}{(k-1)!(n-k)!}[F(x)]^{k-1}[F(x+\Delta x)-F(x)][1 - F(x+\Delta x)]^{n-k}$

Letting $\Delta x\rightarrow 0$ , we have

$p_k(x) = \dfrac{n!}{(k-1)!(n-k)!}[F(x)]^{k-1}p_x(k)[1 - F(x)]^{n-k}$

Example 2

Now suppose $\xi_1, \xi_2, ..., \xi_n$ are $n$ samples from $\xi$ , $\xi_{(1)}, \xi_{(2)}, ..., \xi_{(n)}$ are ordered statistical quantities. For any $x$ , denoting

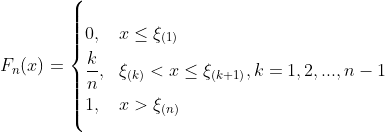
Then $F_n(x)$ is called the empirical distribution function of $\xi$ . Further introducing step function $\mu(x)$ , then the above equation can be written as

$F_n(x) = {\displaystyle \dfrac{1}{n}\sum_{k=1}^n\mu(x-\xi_k)},\ \ x\in R$

## Table of Contents

Twitter Facebook LinkedIn

Chao Huang

Statistics [06]: Order Statistics

Example 1

Example 2

Comments