Statistics [07]: Multivariate Normal Distributions

1 minute read

Published: January 07, 2021

Bivariate and multivariate normal distributions.

Bivariate Distributions

The two variables in a bivariate normal are both are normally distributed, and they have a normal distribution when both are added together. Visually, the bivariate normal distribution is a three-dimensional bell curve.

A bivariate normal distribution can be expressed as

$(X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2, \rho)$

where $\rho)$ is the correlation coefficient between $X$ and $Y$ . And the probability density function is

$p(x,y) = \dfrac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\left\{-\dfrac{1}{2(1-\rho^2)}\left[\dfrac{(x-\mu_1)^2}{\sigma_1^2}-2\rho\dfrac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2}+\dfrac{(y-\mu_2)^2}{\sigma_2^2}\right]\right\}$

Let

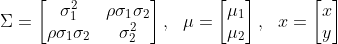
The above equation can be reformulated as

$p(x,y) = \dfrac{1}{2\pi|\Sigma|^{1\text{/}2}}\exp\left\{-\dfrac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right\}$

Example

A bivariate normal distribution satisfies $(X,Y)=N\left(0,0,1,\dfrac{1}{4},\dfrac{1}{3}\right)$ , assume $U = X-2Y$ and $V=X+2Y$ , find $E(X^2|V=0)$ .

Firstly,

$cov(U,V)=cov((X-2Y)(X+2Y)) = cov(X,X)-4cov(Y,Y) = 0$ .

Hence, $U$ and $V$ are independent and

$X = \dfrac{U+V}{2}$

Therefore,

$E(X^2|V=0) = E\left(\left(\dfrac{U+V}{2}\right)^2|V=0\right) = E\left(\dfrac{U}{2}\right)^2 = \dfrac{1}{4}E(X^2 + Y^2 - 4XY) = \dfrac{1}{3}$

Multivariate Normal Distributions

A multivariate nromal distribution can be expressed as

$\eta \sim N_n(\theta, \Sigma)$

where

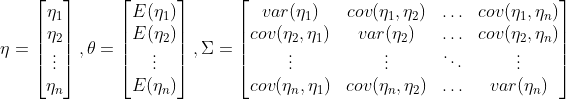
The probability density function would be

$p_\eta(y_1,y_2,...,y_n) = \dfrac{1}{(2\pi)^{n\text{/}2}|\Sigma|^{1\text{/}2}}\exp\left\{-\dfrac{1}{2}(y-\theta)^T\Sigma^{-1}(y-\theta)\right\}$

The sufficient and necessary condition that $\eta_1,\eta_2,...,\eta_n$ are mutually independent is that every two of $\eta_1,\eta_2,...,\eta_n$ are unrelated.

Linear Transformation of Normal Distribution

Property 1

Assume $n$ -dimensional random vector $X\sim N(\mu,\Sigma)$ , $A$ is a $n$ -dimensional invertible matrix, $b\in R^n$ . Then

$Y = AX + b \sim N(A\mu + b, A\Sigma A^T)$ .

Property 2

Assume $n$ -dimensional random vector $X\sim N(\mu,\Sigma)$ , $A$ is a $m\times n$ -dimensional matrix, $\text{Rank}\,A = m$ , $b\in R^m$ . Then

$Y = AX + b \sim N(A\mu + b, A\Sigma A^T)$ .

Property 3

Assume $X_1,X_2,...,X_n$ are independent, $X_i\sim N(\mu_i,\sigma_i^2)$ , $i=1,2,...,n$ , $a_1,a_2,...,a_n, b \in R$ , where $a_1,a_2,...,a_n$ are not all zeros. Then