Statistics [08]: Conditional Distributions and Expectation

1 minute read

Published: January 08, 2021

Conditional distributions and expectation of discrete and continuous random variables.

Conditional Distributions of Discrete Random Variables

Conditional probability of discrete random variables can be expressed as

$p_{i|j} = P(X=x_i|Y=y_j) = \dfrac{P(X=x_i, Y=y_j)}{P(Y=y_j)} = \dfrac{p_{ij}}{p_{.j}}$

where

$P(Y=y_j) = p_{.j} = {\displaystyle \sum_{i=1}^\infty p_{ij}}$

Then, the distribution function of $X$ given $Y=y_j$ is

$F(x|y_j) = {\displaystyle \sum_{x_i\leq x} P(X=x_i|Y=y_j)}$

Additivity of Possion Distributions

Assume $X_1\sim P(\lambda_1)$ , $X_2\sim P(\lambda_2)$ , …, $X_m\sim P(\lambda_m)$ and $X_1$ , $X_2$ , …, $X_m$ are independent, then

$X_1 \+ X_2 \+ ... \+ X_m \sim P(\lambda_1 \+ \lambda_2 \+ ... \+ \lambda_m)$

Proof. For any non-negative $n$ ,

$P(X+ Y = n) = {\displaystyle \sum_{k=0}^n P(X=k, Y=n-k) = \sum_{k=0}^nP(X=k)P(Y=n-k)}$

Hence,

$P(X+ Y = n) = {\displaystyle \sum_{k=0}^n\dfrac{\lambda_1^k}{k!}e^{-\lambda_1}\dfrac{\lambda_2^{n-k}}{(n-k)!}e^{-\lambda_2}} = \dfrac{e^{-(\lambda_1 + \lambda_2)}}{n!}{\displaystyle \sum_{k=0}^n \dfrac{n!}{k!(n-k)!}\lambda_1^k\lambda_2^{n-k}} = \dfrac{e^{-(\lambda_1 + \lambda_2)}}{n!}(\lambda_1+\lambda_2)^n$

Therefore,

$X+ Y\sim P(\lambda_1 + \lambda_2)$

Additivity of Binomial Distributions

Assume $X_1\sim B(n_1,p)$ , $X_2\sim B(n_2,p)$ , …, $X_m\sim B(n_m,p)$ and $X_1$ , $X_2$ , …, $X_m$ are independent, then

$X_1 \+ X_2 \+ ... \+ X_m \sim B(n_1 \+ n_1 \+ ... \+ n_m, p)$

Proof. For any non-negative $n$ ,

$P(X+ Y = n) = {\displaystyle \sum_{k=0}^n \dbinom{n_1}{k}p^k(1-p)^{n_1-k}\dbinom{n_2}{n-k}p^{n-k}(1-p)^{n_2+k-n} = \sum_{k=0}^n \dbinom{n}{n_1+ n_2}p^n(1-p)^{n_2+n_2-n}}$

Therefore,

$X+ Y\sim B(n_1 + n_2, p)$

Example 1

Assume $X$ and $Y$ are independent, $X\sim P(\lambda_1)$ , $Y\sim P(\lambda_2)$ . Find the conditional distribution of $X$ given $X+ Y=n$ .

Solution.

$P(X=k|X+ Y=n) = \dfrac{P(X=k, Y=n-k)}{P(X+ Y =n)} = \dfrac{ \dfrac{\lambda_1^k}{k!}e^{-\lambda_1}\dfrac{\lambda_2^{n-k}}{(n-k)!}e^{-\lambda_2}}{\dfrac{(\lambda_1 + \lambda_2)^n}{n!}e^{-(\lambda_1+\lambda_2)}} = \dbinom{n}{k}\dfrac{\lambda_1^k\lambda_2^{n-k}}{(\lambda_1+\lambda_2)^n}$

Therefore,

$P(X=k|X+ Y=n) =B\left(n, \dfrac{\lambda_1}{\lambda_1 + \lambda_2} \right)$

Conditional Distribution of Continuous Random Variables

For any $p_Y(y) > 0$ , the conditional distribution function of $X$ given $Y=y$ is

$F(x|y) = P(X\leq x| Y=y) = {\displaystyle \lim_{h\to 0}P(X\leq x|y\leq Y\leq Y+ h) = \lim_{h\to 0}\dfrac{P(X\leq x, y \leq Y\leq y+ h)}{P(y\leq Y \leq y+ h)}}$

where

$\lim_{h\to 0}P(X\leq x|y\leq Y\leq Y+ h) = \lim_{h\to 0}\int_{-\infty}^x du\int_y^{y+ h}p(u,v)dv = \lim_{h\to 0}\int_{-\infty}^x(p(u,y +c_1h)h)du$

and

$\lim_{h\to 0}P(y\leq Y \leq y+ h) = \lim_{h\to 0}\int_y^{y+ h}p_Y(v)dv =\lim_{h\to 0} \int_y^{y + h}p_Y(y + c_2h)h$

Hence,

$F(x|y) ={\displaystyle \dfrac{\int_{-\infty}^xp(u,y)du}{p_Y(y)} = \int_{-\infty}^x\dfrac{p(u,y)}{p_Y(y)}du}$

Therefore, the probability density function is

$P(x|y) ={\displaystyle \dfrac{p(x,y)}{p_Y(y)} \sim p_{X|Y}(x|y)}$

Example 2

Assume $(X,Y)$ has a uniform distribution on $G=\left\{ (x,y); x^2 + y^2 \leq 1 \right\}$ , find $p(x|y)$ .

Solution.

$p(x, y) = \dfrac{1}{\pi}, x^2 + y^2 \leq 1$

$p_Y(y) = {\displaystyle \int_{-\infty}^{\infty}p(x,y)dx = \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}\dfrac{1}{\pi}dx = \dfrac{2}{\pi}\sqrt{1-y^2}, -1\leq y \leq 1}$

Therefore,

$p(x|y) = \dfrac{p(x,y)}{p_Y(y)} = \dfrac{1}{2\sqrt{1-y^2}}, |y|\leq 1, x^2 + y^2 \leq 1$

Example 3

Assume $(X,Y)$ has a bivariate normal distribution $N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)$ , find $p(y|x)$ .

Solution.

$p(x, y) = \dfrac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\left\{\dfrac{-1}{2(1-\rho^2)}\left[\dfrac{(x-\mu_1)^2}{\sigma_1^2} - 2\rho\dfrac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2} + \dfrac{(y-\mu_2)^2}{\sigma_2^2}\right]\right\}$

$p_X(x) = \dfrac{1}{\sqrt{2\pi}\sigma_1}\exp\left\{-\dfrac{(x-\mu_1)^2}{2\sigma_1^2}\right\}$

Hence,

$p(y|x) = \dfrac{1}{\sqrt{2\pi}\sigma_2\sqrt{1-\rho^2}}\exp\left\{\dfrac{-1}{2(1-\rho^2)}\left[\dfrac{(x-\mu_1)^2}{\sigma_1^2} - 2\rho\dfrac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2} + \dfrac{(y-\mu_2)^2}{\sigma_2^2} - \dfrac{(1-\rho^2)(x-\mu_1)^2}{\sigma_1^2}\right]\right\}$

$p(y|x) = \dfrac{1}{\sqrt{2\pi}\sigma_2\sqrt{1-\rho^2}}\exp\left\{\dfrac{-1}{2\sigma_2^2(1-\rho^2)}\left[(y-\mu_2) - \rho\dfrac{\sigma_2}{\sigma_1}(x-\mu_1)\right]^2\right\}$

Therefore,

$p(y|x) \sim N\left( \mu_2 + \rho\dfrac{\sigma_2}{\sigma_1}(x-\mu_1), \sigma_2^2(1-\rho^2) \right)$

Conditional Expectation

For discrete random variables,

$E(X|Y=y) = {\displaystyle \sum_ix_iP(X=x_i|Y=y)}$

For continuous random variables,

$E(X|Y=y) = {\displaystyle \int_{-\infty}^{\infty}xP(x|y)dx}$

Example 4

Assume $X\sim Ge(\dfrac{1}{4})$ , find $E(X|X>3)$ .

Solution.

$E(X|X>3) = {\displaystyle \sum_{k=1}^\infty (k+3)P(X=k+3|X>3) = \sum_{k=1}^\infty (k+3)P(X=k)}$

$E(X|X>3) = {\displaystyle \sum_{k=1}^\infty kP(X=k) + \sum_{k=1}^\infty 3 P(X=k) = 4 + 3 = 7}$

Note that $E(X|Y)$ is a random variable!

Example 5

Assume $X\sim Ge(p)$ and $\{Y=1,\ \ \text{when}\ \ X=1;Y=0,\ \ \text{when} \ \ X>1\}$ , find $E(X|Y)$ .

Solution.

$E(X|Y=0) = E(X|X>1) = 1 + \dfrac{1}{p}, E(X|Y=1) = E(X|X=1) = 1$

$P(Y=1) = p, P(Y=0) = 1-p$

Therefore,

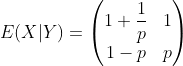
drawing

From example 5, we have

$E(E(X|Y)) = (1 + \dfrac{1}{p})(1-p) + p = \dfrac{1}{p}$

This equation is called law of total expectation, which says

$E(E(X|Y)) = E(X)$

Proof.

$E(X) = {\displaystyle \int_{-\infty}^\infty xp_x(x)dx = \int_{-\infty}^\infty x\int_{-\infty}^\infty p(x,y)dydx = \int_{-\infty}^\infty x\int_{-\infty}^\infty p_Y(y)p(x|y)dydx = \int_{-\infty}^\infty p_Y(y)dy\int_{-\infty}^\infty xp(x|y)dx}$

Hence,

$E(X) = {\displaystyle \int_{-\infty}^\infty E(X|Y=y)p_Y(y)dy = E(E(X|Y))}$

Example 6

For example 5, find $var(X)$ .

Solution.

$E(X^2) = E(E(X^2|Y)) = P(X=1)E(X^2|X=1) + P(X>1)E(X^2|X>1)$

where

$E(X^2|X=1) = 1, E(X^2|X>1)=E((1+X)^2) = 1 + 2E(X) + E(X^2)$

Hence,

$E(X^2) = p + (1-p)(1+ \dfrac{2}{p}+ E(X^2)) \Rightarrow E(X^2) = \dfrac{2}{p^2} - \dfrac{1}{p}$

Therefore,

$var(X) = E(X^2)-E^2(X) = \dfrac{1}{p^2} - \dfrac{1}{p}$

Example 7

Assume $X_1,X_2,...,X_n$ are commonly independent random variables, $N$ is a integer random variable. Prove that $E{\displaystyle \left( \sum_{k=1}^N X_k \right) = E(X_1)E(N)}$ .

Proof.

$E{\displaystyle \left( \sum_{k=1}^N X_k \right) = E\left( E\left( \sum_{k=1}^N X_k|N \right) \right) = \sum_{n=1}^\infty P(N=n)E\left( \sum_{k=1}^N X_k|N=n \right)}$

As $X_1,X_2,...,X_n$ are commonly independent, we have

$E{\displaystyle \left( \sum_{k=1}^N X_k \right) = \sum_{n=1}^\infty P(N=n)nE(X_1) = E(X_1)E(N)}$

Twitter Facebook LinkedIn

Chao Huang

Statistics [08]: Conditional Distributions and Expectation

Conditional Distributions of Discrete Random Variables

Additivity of Possion Distributions

Additivity of Binomial Distributions

Example 1

Conditional Distribution of Continuous Random Variables

Example 2

Example 3

Conditional Expectation

Example 4

Example 5

Example 6

Example 7

Table of Contents

Comments