Statistics [25]: From Uniform to General Distributions

1 minute read

Published: January 25, 2021

General practice of converting a uniform distribution to a general distribution.

Theorem

Assume $X\sim U[0,1]$ , function $F$ is a monotone increasing function, and for $\forall y\in R$ ,

$F(-\infty) = 0 \leq F(y) \leq 1 = F(\infty)$

Then, the probability distribution function of $Y = F^{-1}(X)$ is $F(y)$ .

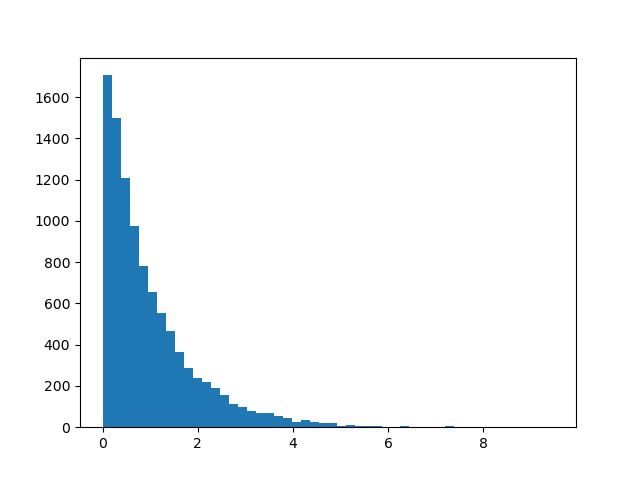
Example 1

Generate an exponential distribution with parameter $\lambda$ from uniform distribution $U[0,1]$ .

Firstly, the probability distrbution function of the exponential function is

$F(y) = 1 - e^{-\lambda y}$

It can be easily verified that $F(y)$ is a monotone increasing function, hence

$y = F^{-1}(x) = -\dfrac{\ln(1-x)}{\lambda}, X\sim U[0,1]$

which can be used to generate random number conforming an exponential distribution with parameter $\lambda$ .

To test this,

$F(y) = P(Y\leq y) = P\left(\dfrac{-\ln(1-X)}{\lambda}\leq y\right)=P(X\leq 1-e^{-\lambda Y}) = 1-e^{-\lambda y}$

This proved the conclusion.

# uniform to exponential
lambdaE = 1
x = np.random.random(10000)
y = -np.log(1-x)/lambdaE
plt.hist(y,bins=50)
plt.show()

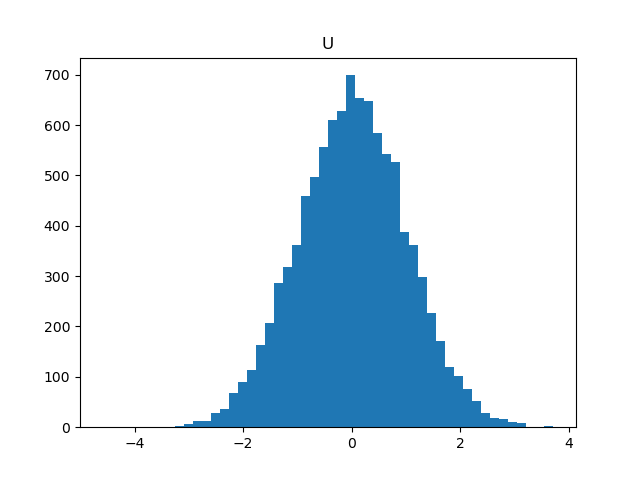
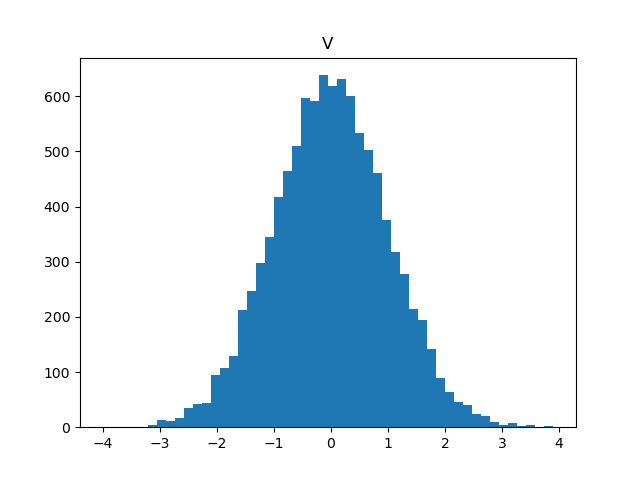
drawing

Example 2 - Box-Muller Method

Assume $X,Y \sim U[0,1]$ are independent, make the transform $U = (-2\ln X)^{1\text{/}2}\cos 2\pi Y$ and $V = (-2\ln X)^{1\text{/}2}\sin 2\pi Y$ , then $U, V$ are also independent and follow the standard normal distribution.

Proof is easy and is thus omitted here.

# uniform to normal
x = np.random.random(10000)
y = np.random.random(10000)
U = (-2*np.log(x))**0.5*np.cos(2*np.pi*y)
V = (-2*np.log(x))**0.5*np.sin(2*np.pi*y)

plt.figure()
plt.hist(U,bins=50)
plt.title('U')
plt.show()

plt.figure()
plt.hist(V,bins=50)
plt.title('V')
plt.show()

drawing

Von Neumann Rejection Sampling

Generate random numbers with probability density function $p(x)$ .

Suppose that we know an upper bound for $p(x)$ and a proposal distribution $q(x)$ , so that there is $c<\infty$ such that $p(x)<cq(x)$ .

Here is the algorithm:

Draw a sample u ~ U[0,1]
Draw a sample x ~ q(x)
if p(x) / (cq(x)) >= u then
  accept x
else
  reject it and repeat
endif

Theorem

Assume $\eta\sim q(x)$ and $u\sim U[0,1]$ , $\eta$ and $u$ are independent, then

$P\left(\eta \leq x\Big|\dfrac{p(\eta)}{cq(\eta)}\geq u\right) = {\displaystyle \int_{-\infty}^xp(y)dy}$

Proof. Use the law of total probability.

$P\left(\eta \leq x\Big|\dfrac{p(\eta)}{cq(\eta)}\geq u\right) = {\displaystyle \dfrac{P\left(\eta\leq x, \dfrac{p(\eta)}{cq(\eta)}\geq u\right)}{P\left(\dfrac{p(\eta)}{cq(\eta)}\geq u\right)} = \dfrac{\int_{-\infty}^\infty P\left(\eta\leq x,\dfrac{p(\eta)}{cq(\eta)}\geq u\Big|\eta=y\right)q(y)dy}{\int_{-\infty}^\infty P\left(\dfrac{p(\eta)}{cq(\eta)}\geq u\Big|\eta=y\right)q(y)dy}}$

$= {\displaystyle \dfrac{\int_{-\infty}^x P\left(\dfrac{p(y)}{cq(y)}\geq u\right)q(y)dy}{\int_{-\infty}^\infty P\left(\dfrac{p(y)}{cq(y)}\geq u\right)q(y)dy} = \dfrac{\int_{-\infty}^x \dfrac{p(y)}{cq(y)}q(y)dy}{\int_{-\infty}^\infty\dfrac{p(y)}{cq(y)}q(y)dy} = \int_{-\infty}^xp(y)dy}$

Twitter Facebook LinkedIn

Chao Huang

Statistics [25]: From Uniform to General Distributions

Theorem

Example 1

Example 2 - Box-Muller Method

Von Neumann Rejection Sampling

Theorem

Table of Contents

Comments