Statistics [28]: Multiple Regression Model

10 minute read

Published: January 28, 2021

The purpose of multiple regression model is to estimate the dependent variable (response variable) using multiple independent variables (explanatory variables).

Multiple Regression Model

Notation

Suppose there are $n$ subjects and data is collected from these subjects.

Data on the response variable is $y_1,y_2,...,y_n$ , which is represented by the column vector $Y=(y_1,y_2,...,y_n)^T$ .

Data on the $j\text{th}\,(j=1,2,...,p)$ explanatory variable $x_j$ is $x_{1j},x_{2j},...,x_{nj}$ , which is represented by the $n\times p$ matrix $X$ . The $i\text{th}$ row of $X$ has data collected from the $i\text{th}$ subject and the $j\text{th}$ column of $X$ has data for the $j\text{th}$ variable.

The Linear Model

The linear model is assumed to have the following form:

$y_i = \beta_1x_{i1} + \beta_2x_{i2} + \cdots + \beta_px_{ip}+ e_i,\ \ i=1,2,...,n$

where $e_i \sim N(0,\sigma^2)$ .

In matrix notation, the model can be written as

$Y = X\beta + e$

The Intercept Term

The linear model stipulates that $E(y_i) = \beta_1x_{i1} + \beta_2x_{i2} + \cdots + \beta_px_{ip}$ , which implies that when $x_{i1}=x_{i2}=\cdots = x_{ip}=0$ , then $E(y_i)=0$ . This is not a reasonable assumption. Therefore, we usually add a intercept term to the model such that

$E(y_i) = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \cdots + \beta_px_{ip}$

Further, let $x_{i0}=1$ , the above equation can be rewritten as

$E(y_i) =\beta_0x_{i0}+ \beta_1x_{i1} + \beta_2x_{i2} + \cdots + \beta_px_{ip}$

In matrix notation,

$Y = X\beta + e$

where $X$ now denotes the $n\times (p+ 1)$ matrix whose first column consists of all ones and $\beta = (\beta_0,\beta_1,...\beta_p)^T$ .

Estimation

Similar to the unitary regression model, $\beta$ is estimated by minimizing the residual sum of squares:

$S(\beta) = {\displaystyle \sum_{i=1}^n(y_i-\beta_0-\beta_1x_{i1}-\cdots -\beta_px_{ip})^2}$

In matrix notation,

$S(\beta) = \left\|Y-X\beta\right\|^2$

Using this notation, we have

$S(\beta) = (Y-X\beta)^T(Y-X\beta) = Y^TY - 2\beta^TX^TY + \beta^TX^TX\beta$

Take partial derivatives with respect to $\beta_i$ yields

$\nabla S(\beta) = 2X^TX\beta - 2X^TY = 0 \Rightarrow X^TX\beta = X^TY$

This gives $p$ linear equations for the $p$ unknown $\beta_i,i=1,2,...,p$ . The solution is denoted as $\hat{\beta} = (\hat{\beta}_1,\hat{\beta}_2,...,\hat{\beta}_p)^T$ .

As $X^TY$ lies in the column space of $X^T$ , there is always solution(s). And if $X^TX$ is invertible, there will be a unique solution, which is given by $\hat{\beta} = (X^TX)^{-1}X^TY$ .

In fact, $X^TX$ being invertible is equivalent to $\text{rank}(X) = p+ 1$ . Thus when $X^TX$ is non-invertible, $\text{rank}(X) < p+ 1$ . In other words, some columns of $X$ is a linear combination of the other columns. Hence, some explanatory variables would be redundant.

Properties of the Estimator

Assume $X^TX$ is invertible, the estimator $\hat{\beta}$ has the following properties.

Linearity

An estimator is said to be linear if it can be written as $AY$ .

Unbiasedness

$E(\hat{\beta}) = E((X^TX)^{-1}X^TY) = (X^TX)^{-1}X^TE(Y) = (X^TX)^{-1}X^TX\beta = \beta$

Covariance

$cov(\hat{\beta}) = cov((X^TX)^{-1}X^TY) = (X^TX)^{-1}X^Tcov(Y)X(X^TX)^{-1} = \sigma^2(X^TX)^{-1}$

where

$cov(Y) = E[(Y-E(Y))(Y-E(Y))^T] = E[(X\beta+ e - X\beta)(X\beta+ e - X\beta)^T] = \sigma^2I$

Optimality

The Gaussian-Markov Theorem states that $\beta$ is the best linear unbiased estimator.

Fitted Values

Given the model, the fitted value can be written in matrix form as

$\hat{Y} = X\hat{\beta} = X(X^TX)^{-1}X^TY$

which can be seen as the orthogonal projection of $Y$ onto the column space of $X$ .

Let $H = X(X^TX)^{-1}X^T$ such that $\hat{Y} = HY$ , the matrix $H$ is called the Hat Matrix, which has the following properties:

It is summetric
It is idempotent, $H^2=H$
$HX=X$
$\text{rank}(H) = \text{rank}(X)$

With these properties, we can easily get

$E(\hat{Y}) = E(HY) = HE(Y) = HX\beta = X\beta = E(Y)$

$cov(\hat{Y}) = cov(HY) = Hcov(Y)H^T = \sigma^2H$

Residual

The residual of multiple regression

$\hat{e} = Y - \hat{Y} = (I-H)Y$

It can be verified that the residuals are orthogonal to the column space of $X$ , such that

$\hat{e}^TX = ((I-H)Y)^TX = Y^T(I-H)X = Y^T(X-HX) = 0$

As the first column of $X$ is all ones, it implies that

$\sum_{i=1}^n\hat{e}_i = 0$

Because $\hat{Y} = X\hat{\beta}$ , $\hat{e}$ is also orthogonal to $\hat{Y}$ .

The expectation of $\hat{e}$ is

$E(\hat{e}) = E((I-H)Y) = (I-H)E(Y) = (I-H)X\beta = (X-HX)\beta=0$

The covariance matrix of $\hat{e}$ is

$cov(\hat{e}) = cov((I-H)Y) = (I-H)cov(Y)(I-H) = \sigma^2(I-H)$

Analysis of Variance

Similar to the unitary regression model,

$\sum_{i=1}^n(y_i-\bar{y})^2 = \sum_{i=1}^n(\hat{y}_i-\bar{y})^2 + \sum_{i=1}^n(y_i-\hat{y}_i)^2} \Rightarrow \text{TSS} = \text{RegSS} + \text{RSS$

with

$\text{TSS} = {\displaystyle \sum_{i=1}^n(y_i-\bar{y})^2}$

$\text{RSS} = {\displaystyle \sum_{i=1}^n(y_i-\hat{y})^2}$

$\text{RegSS} = {\displaystyle \sum_{i=1}^n(\hat{y}_i-\bar{y})^2}$

As there are $p+ 1$ parameters in the model, we have

$\dfrac{\text{RSS}}{\sigma^2}\sim \chi^2(n-p-1)$

Thus, the confidence interval of $\sigma^2$ is

$\left[\dfrac{\text{RSS}}{\chi^2_{1-\alpha\text{/}2}(n-p-1)},\dfrac{\text{RSS}}{\chi^2_{\alpha\text{/}2}(n-p-1)}\right]$

The R-Squared is similarly defined as

$R^2 = \dfrac{\text{RegSS}}{\text{TSS}} = 1 - \dfrac{\text{RSS}}{\text{TSS}}$

and the adjusted R-Squared is defined as

$R_a^2 =1 - \dfrac{\text{RSS}/(n-p-1)}{\text{TSS}/(n-1)}$

If $R^2$ is high, it means that RSS is much smaller compared to TSS and hence the explanatory variables are really useful in predicting the response.

Expected Value of RSS

Firstly,

$\text{RSS} = \hat{e}^T\hat{e} = Y^T(I-H)Y = e^T(I-H)e$

Hence,

$E(RSS) = E(e^T(I-H)e) = E\left(\sum_{i\text{,}j}(I-H)_{i\text{,}j}e_ie_j\right) = \sum_{i\text{,}j}(I-H)_{i\text{,}j}E(e_ie_j)$

As $E(e_ie_j)=0, i\neq j; E(e_ie_j)\sigma^2, i=j$ , we have

$E(RSS) = {\displaystyle \sigma^2\sum_{i=1}^n(I-H)_{i\text{,}i} = \sigma^2\left(n-\sum_{i=1}^nH_{i\text{,}i}\right) = \sigma^2(n-tr(H))}$

As $tr(H) = tr(X(X^TX)^{-1}X^T) = tr(X^TX(X^TX)^{-1}) = tr(I_{p+ 1}) = p+ 1$ , we get

$E(RSS) = \sigma^2(n-p-1)$

Therefore, an unbiased estimator of $\sigma^2$ is given by

$\hat{\sigma}^2 = \dfrac{\text{RSS}}{n-p-1}$

This also implies that

$\dfrac{\text{RSS}}{\sigma^2} \sim \chi^2(n-p-1)$

Properties

We assume that $e\sim N_n(0,\sigma^2I_n)$ . Equivalently, $e_1,e_2,...,e_n$ are independent normals with mean 0 and variance $\sigma^2$ .

Distribution of $Y$

Since $Y=X\beta + e$ , we have $Y\sim N_n(X\beta,\sigma^2I_n)$

Distribution of $\hat{\beta}$

Since $E(\hat{\beta}) = \beta$ and $cov(\hat{\beta}) = \sigma^2(X^TX)^{-1}$ , we have $\hat{\beta} \sim N_{p+ 1}(\beta,\sigma^2(X^TX)^{-1})$

Distribution of Fitted Values

As $E(\hat{Y})=E(HY) = X\beta$ and $cov(\hat{Y})=cov(HY)=\sigma^2H$ , we have $\hat{Y} \sim N_n(X\beta,\sigma^2H)$

Distribution of Residuals

As $E(\hat{e}) = E((I-H)Y) = 0$ and $cov(\hat{e}) = \sigma^2(I-H)$ , we have $\hat{e} \sim N_n(0,\sigma^2(I-H))$

Distributions of RSS

As $\text{RSS} = \hat{e}^T\hat{e} = Y^T(I-H)Y = e^T(I-H)e$ , we have $\dfrac{\text{RSS}}{\sigma^2} = \left(\dfrac{e}{\sigma}\right)^T(I-H)\left(\dfrac{e}{\sigma}\right)$ . And because $\dfrac{e}{\sigma}\sim N_n(0,1)$ and $I-H$ is symmetric and idempodent with rank $n-p-1$ , we have $\dfrac{\text{RSS}}{n-p-1}\sim \chi^2(n-p-1)$

Independence of Residuals $\hat{e}$ and $\hat{\beta}$

To prove the independence of $\hat{e}$ and $\hat{\beta}$ , we can use the theorem below.

Theorem. Let $U\sim N_n(\mu,\Sigma)$ and $A$ be a fixed $k\times n$ matrix and $B$ be a fixed $l\times n$ matrix. Then, $AU$ and $BU$ are independent if and only if $A\Sigma B^T = 0$ .

To prove the theorem, let $Y = [A; B] U = [AU; BU]$ . From the properties of the multivariate normal distribution, $cov(Y) = [A; B]\Sigma[A^T\ \ B^T] = [A\Sigma A^T\ \ A\Sigma B^Y; B\Sigma A^T\ \ B\Sigma B^T]$ . Hence, $AU$ and $BU$ are uncorrelated if and only if $A\Sigma B^T = 0$ .

Because $\hat{e} = (I-H)Y$ and $\hat{\beta} = (X^TX)^{-1}X^TY$ , let $A = I-H$ , $B=(X^TX)^{-1}X^T$ , $U=Y$ and $\Sigma = \sigma^2I$ , then

$A\Sigma B^T = \sigma^2(I-H)X(X^TX)^{-1} = (X-HX)(X^TX)^{-1} = 0$

Thus, we can conclude that $\hat{e}$ and $\hat{\beta}$ are independent.

Simipliarly, as $\hat{Y} = HY$ , let $B=H$ , we have

$A\Sigma B^T = \sigma^2(I-H)H^T = H-H=0$

Thus, we can also conclude that $\hat{e}$ and $\hat{Y}$ are independent.

Significance Test

F-Test

The null hypothesis would be

$H_0: \beta_j = 0$

This means that the explanatory variable $x_{j}$ can be dropped from the linear model, let’s call this reduced model $m$ , and let’s call the original model $M$

It is always true that $\text{RSS}(M)\leq \text{RSS}(m)$ . If $\text{RSS}(M)$ is much smaller than $\text{RSS}(m)$ , it means that the explanatory variable $x_j$ contributes a lot to the regression and hence cannot be dropped. Therefore, we can test $H_0$ via the test statistic:

$\text{RSS}(m) - \text{RSS}(M)$

It can be proved that

$\dfrac{\text{RSS}(m)-\text{RSS}(M)}{\sigma^2} \sim \chi^2(1)$

Hence, the $F$ statistica would be

$\dfrac{\text{RSS}(m)-\text{RSS}(M)}{\text{RSS}(M)/(n-p-1)}\sim F(1,n-p-1)$

More generally, $q$ be the number of explanatory variables in $m$ , we have

$\dfrac{\text{RSS}(m)-\text{RSS}(M)}{\sigma^2} \sim \chi^2(p-q)$

To prove this, denote the hat matrix $H$ in the two models by $H(m)$ and $H(M)$ , then

$\text{RSS}(m) = Y^T(I-H(m))Y, \text{RSS}(M)=Y^T(I_H(M))Y \Rightarrow \text{RSS}(m)-\text{RSS}(M) = Y^T(H(M) - H(m))Y$

Assume $Y=X(m)\beta(m)+ e$ , we should have $H(m)X(m)=X(m)$ and $H(M)X(m)=X(m)$ . Hence,

$\text{RSS}(m)-\text{RSS}(M) = e^T(H(M) - H(m))e$

where $\text{rank}(H(M) - H(m))=p-q$ and it is also idempotent since

$(H(M)-H(m))^2 = H(M) + H(m) - 2H(M)H(m) = H(M)-H(m)$

Therefore, under the null hypothesis

$\dfrac{\text{RSS}(m)-\text{RSS}(M)}{\sigma^2} = \left(\dfrac{e}{\sigma}\right)^T(H(M)-H(m))\dfrac{e}{\sigma} \sim \chi^2(p-q)$

We can thus obtain the $F$ statistic

$\dfrac{(\text{RSS}(m)-\text{RSS}(M))/(p-q)}{\text{RSS}(M)/(n-p-1)} \sim F(p-q,n-p-1)$

Specially, when $\beta_1=\beta_2=\cdots = \beta_p=0$ , the model becomes $y_i=\beta_0 + e_i$ . In this case, $\text{RSS}(m)=\text{TSS}, \text{RSS}(M)=\text{RSS}$ and $q=0$ . Thus the $F$ statistic would be

$\dfrac{(\text{TSS}-\text{RSS})/p}{\text{RSS}/(n-p-1)} \sim F(p,n-p-1)$

And the $p$ value would be

$P\left(F(p,n-p-1) > \dfrac{(\text{TSS}-\text{RSS})/p}{\text{RSS}/(n-p-1)}\right)$

t-Test

Under normality of the errors, we have $\hat{\beta} \sim N_{p+ 1}(\beta,\sigma^2(X^TX)^{-1})$ , Hence,

$\hat{\beta}_j\sim N(\beta_j,\sigma^2v_j)$

where $v_j$ is the $j\text{th}$ diagonal entry of $(X^TX)^{-1}$ . Under the null hypothesis when $\beta_j = 0$ , we have

$\dfrac{\hat{\beta}_j}{\sigma\sqrt{v_j}}\sim N(0,1)$

This can be used to construct the $t$ statistic

$\dfrac{\hat{\beta}_j/(\sigma\sqrt{v_j})}{\sqrt{\text{RSS}/((n-p-1)\sigma^2)}} = \dfrac{\hat{\beta}_j/\sqrt{v_j}}{\sqrt{\text{RSS}/(n-p-1)}}=\sim t(n-p-1)$

$p$ value for testing $H_0: \beta_j=0$ can be got by

$P\left(|t(n-p-1)|>\left|\dfrac{\hat{\beta}_j/\sqrt{v_j}}{\sqrt{\text{RSS}/(n-p-1)}}\right|\right)$

Example

Data

Below is the medical test results of 14 diabetes, build a model to predict the blood sugar level based on other factors.

Number	Cholesterol (mmol/L)	Triglycerides (mmol/L)	Insulin (muU/ml)	Glycated Hemoglobin (%)	Blood Sugar (mmol/L)
1	5.68	1.90	4.53	8.20	11.20
2	3.79	1.64	7.32	6.90	8.80
3	6.02	3.56	6.95	10.80	12.30
4	4.85	1.07	5.88	8.30	11.60
5	4.60	2.32	4.05	7.50	13.40
6	6.05	0.64	1.42	13.60	18.30
7	4.90	8.50	12.60	8.50	11.10
8	5.78	3.36	2.96	8.00	13.60
9	5.43	1.13	4.31	11.30	14.90
10	6.50	6.21	3.47	12.30	16.00
11	7.98	7.92	3.37	9.80	13.20
12	11.54	10.89	1.20	10.50	20.00
13	5.84	0.92	8.61	6.40	13.30
14	3.84	1.20	6.45	9.60	10.40

Regression

Linear regression using statsmodels.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm

data = np.array([[5.68,3.79,6.02,4.85,4.60,6.05,4.90,5.78,5.43,6.50,7.98,11.54,5.84,3.84],
                 [1.90,1.64,3.56,1.07,2.32,0.64,8.50,3.36,1.13,6.21,7.92,10.89,0.92,1.20],
                 [4.53,7.32,6.95,5.88,4.05,1.42,12.60,2.96,4.31,3.47,3.37,1.20,8.61,6.45],
                 [8.20,6.90,10.8,8.30,7.50,13.6,8.50,8.00,11.3,12.3,9.80,10.50,6.40,9.60],
                 [11.2,8.80,12.3,11.6,13.4,18.3,11.1,13.6,14.9,16.0,13.20,20.0,13.3,10.4]])
dataDF = pd.DataFrame(np.transpose(data),columns = ['X1','X2','X3','X4','Y'])  

Y = dataDF['Y']
X = dataDF[['X1','X2','X3','X4']]
X = sm.add_constant(X)
model = sm.OLS(Y,X)
results = model.fit()

results.summary()

Results:

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      Y   R-squared:                       0.797
Model:                            OLS   Adj. R-squared:                  0.707
Method:                 Least Squares   F-statistic:                     8.844
Date:                Wed, 09 Mar 2022   Prob (F-statistic):            0.00349
Time:                        21:23:23   Log-Likelihood:                -23.816
No. Observations:                  14   AIC:                             57.63
Df Residuals:                       9   BIC:                             60.83
Df Model:                           4                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          3.1595      4.308      0.733      0.482      -6.587      12.906
X1             1.1329      0.492      2.304      0.047       0.021       2.245
X2            -0.2042      0.245     -0.833      0.427      -0.759       0.351
X3            -0.1349      0.237     -0.570      0.583      -0.670       0.400
X4             0.5345      0.257      2.080      0.067      -0.047       1.116
==============================================================================
Omnibus:                        2.606   Durbin-Watson:                   1.337
Prob(Omnibus):                  0.272   Jarque-Bera (JB):                1.114
Skew:                          -0.221   Prob(JB):                        0.573
Kurtosis:                       1.691   Cond. No.                         128.
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

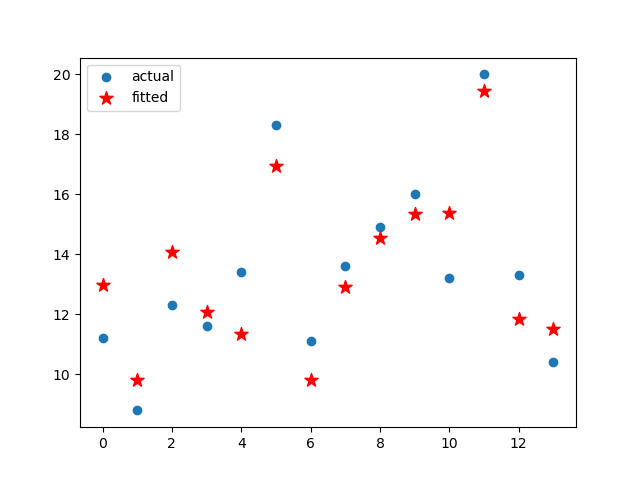
plt.scatter(range(len(Y)),Y,label='actual')
plt.scatter(range(len(Y)),results.fittedvalues,c="r",marker='*',label="fitted",s=10**2)
plt.legend()
plt.show()

drawing

An alternate way is to use functions provided in statsmodels.formula.api, which has the constant term by default.

###
from statsmodels.formula.api import ols
model = ols('Y ~ X1 + X2 + X3 + X4', data=dataDF).fit()

Results:

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      Y   R-squared:                       0.797
Model:                            OLS   Adj. R-squared:                  0.707
Method:                 Least Squares   F-statistic:                     8.844
Date:                Wed, 09 Mar 2022   Prob (F-statistic):            0.00349
Time:                        21:55:34   Log-Likelihood:                -23.816
No. Observations:                  14   AIC:                             57.63
Df Residuals:                       9   BIC:                             60.83
Df Model:                           4                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept      3.1595      4.308      0.733      0.482      -6.587      12.906
X1             1.1329      0.492      2.304      0.047       0.021       2.245
X2            -0.2042      0.245     -0.833      0.427      -0.759       0.351
X3            -0.1349      0.237     -0.570      0.583      -0.670       0.400
X4             0.5345      0.257      2.080      0.067      -0.047       1.116
==============================================================================
Omnibus:                        2.606   Durbin-Watson:                   1.337
Prob(Omnibus):                  0.272   Jarque-Bera (JB):                1.114
Skew:                          -0.221   Prob(JB):                        0.573
Kurtosis:                       1.691   Cond. No.                         128.
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Variable Selection

From the results, we can see that $p$ value of $X2$ and $X3$ are 0.426 and 0.583 respectively, meaning that their influence may not be that dignificant than $X1$ and $X4$ . Therefore, let’s do the regression again considering only $X1$ and $X4$ .

model = ols('Y ~ X1 + X4', data=dataDF).fit()

Results:

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      Y   R-squared:                       0.745
Model:                            OLS   Adj. R-squared:                  0.699
Method:                 Least Squares   F-statistic:                     16.07
Date:                Wed, 09 Mar 2022   Prob (F-statistic):           0.000545
Time:                        22:08:30   Log-Likelihood:                -25.420
No. Observations:                  14   AIC:                             56.84
Df Residuals:                      11   BIC:                             58.76
Df Model:                           2                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept      1.8257      2.253      0.810      0.435      -3.133       6.784
X1             0.9517      0.255      3.729      0.003       0.390       1.513
X4             0.6358      0.237      2.686      0.021       0.115       1.157
==============================================================================
Omnibus:                        1.107   Durbin-Watson:                   1.652
Prob(Omnibus):                  0.575   Jarque-Bera (JB):                0.726
Skew:                           0.048   Prob(JB):                        0.695
Kurtosis:                       1.888   Cond. No.                         57.4
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

plt.scatter(range(len(Y)),Y,label='actual')
plt.scatter(range(len(Y)),results.fittedvalues,c="r",marker='*',label="fitted-full",s=10**2)
plt.scatter(range(len(Y)),model.fittedvalues,c="g",marker='h',label="fitted-reduced",s=10**2,alpha=0.5)
plt.legend()
plt.show()

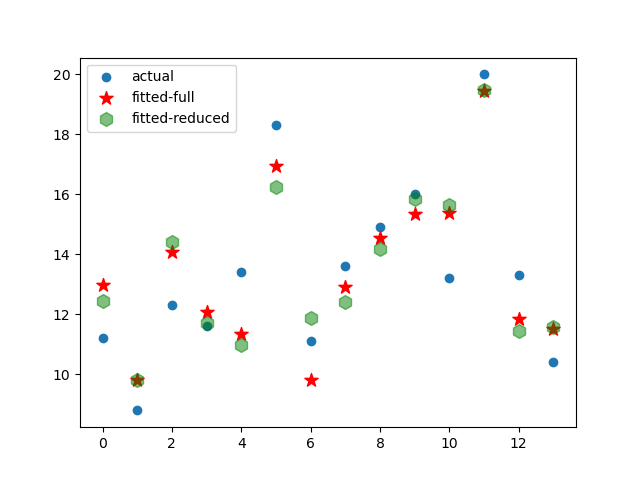
drawing

Twitter Facebook LinkedIn

Chao Huang

Statistics [28]: Multiple Regression Model

Multiple Regression Model

Notation

The Linear Model

The Intercept Term

Estimation

Properties of the Estimator

Linearity

Unbiasedness

Covariance

Optimality

Fitted Values

Residual

Analysis of Variance

Expected Value of RSS

Properties

Significance Test

F-Test

t-Test

Example

Data

Regression

Variable Selection

Table of Contents

Comments